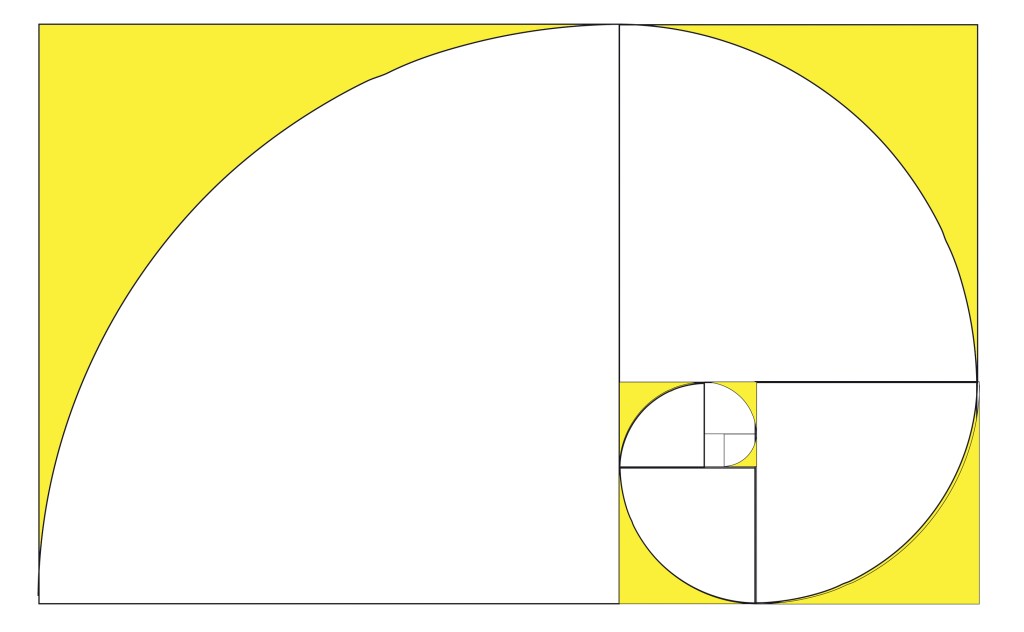
La sezione aurea, è l’unica proporzione matematica in grado di auto generarsi all’infinito. Si tratta di dividere un segmento in due parti diseguali in modo che la parte minore stia alla maggiore come la parte maggiore sta all’intero segmento. Ciò significa che la parte minore rapportata alla parte maggiore darà sempre la misura della stessa suddivisione iniziale, e così via all’infinito.
Questa semplice suddivisione della sezione aurea si può produrre in tanti modi diversi e a partire dagli enti più elementari come il cerchio, il triangolo, il quadrato, ovviamente il pentagono, eccetera, ma la cosa più sorprendente è che essa scaturisce sovente dal rapporto tra enti diversi (come il triangolo con il quadrato), e pertanto è in grado di generare con la sua applicazione forme diversissime in contesti altrettanto diversi. Per questo motivo la sua indagine è ricca di sorprese e di nessi inaspettati, e per lo stesso motivo da epoche remote filosofi, artisti, matematici hanno visto in essa il legame tra il mistero dell’astrazione delle forme e la sua applicazione nella formazione del vivente. Dagli atomi alle galassie, dalle conchiglie fino al corpo umano, dall’architettura alle arti visive, dalla poesia alla musica, la sezione aurea si è portata appresso un bagaglio di conoscenze e scoperte tale da meritarle il nome di “divina proporzione” e di “numero d’oro”…
La ricerca della bellezza nelle arti assomiglia, alla luce della sezione aurea, alla comprensione e applicazione di una sola “regola semplicissima” che dispiega il suo codice in mille forme diverse, dove i dettagli sono sempre riconducibili all’unità, generando una grande armonia che coniuga la varietà delle parti con l’unitarietà dell’insieme.
La sezione aurea è diventata un mito culturale e una specie di campo di prova delle conoscenze, a volte propagando false idee, ma anche tralasciando di approfondirne altre che, ancora oggi, risultano quasi se non del tutto sconosciute. In questo terreno fertile si aggira l’artista con la mentalità dello scienziato, che ricerca il bello ma che non si ferma davanti alle cose presunte note, e così, guardando con i propri occhi, trova cose nuove… Lo scopo è quello di testare le conoscenze e creare nuove immagini capaci di stupirci per la loro semplice complessità, come uno specchio delle nostre strutture e capacità psichiche e cognitive.

Nel famoso Timeo, Platone definisce curiosamente il triangolo “più bello”, e lo fa descrivendolo con il teorema di Pitagora, cioè costruendo i quadrati sui suoi lati. La diagonale BD del quadrato costruito sull’ipotenusa AB del triangolo ABC (che è metà triangolo equilatero, ed è il “triangolo più bello”) taglia il lato del quadrato costruito sul cateto maggiore AC in sezione aurea in E. Sviluppando questa figura è possibile costruire un bellissimo dodecagono regolare, il cui tracciato è variamente suddiviso in sezione aurea.

Il rapporto tra il triangolo e il quadrato, mediato dalla sezione aurea, poteva essere il soggetto del misterioso disegno che Fra Luca Pacioli andava tracciando nel suo misterioso ritratto di inizio del XVI secolo… La figura che il frate matematico va disegnando con la mano destra, non corrisponde alla pagina degli Elementi di Euclide (libro XIII, 8, nell’incunabolo veneziano del 1482 di E. Ratdolt) che viene indicata con la sinistra.

Il rombicubottaedro, il bellissimo solido archimedeo (fatto di soli quadrati e triangoli) sospeso davanti al suo sguardo, cela in sé, come un fatto ancora oggi sconosciuto, la sezione aurea nel rapporto tra le facce quadrate e quelle triangolari. Pacioli sembra in realtà nel suo disegno alludere tout court alla conoscenza della sezione aurea come una prerogativa del triangolo equilatero inscritto in un cerchio, un fatto ignoto per le cronache matematiche dei moderni, che verrà esplicitato solo nel 1983 dall’artista americano G. Odom (con la mediazione del grande geometra del XX secolo H.S.M. Coxeter, amico anche di M.C. Escher). Tuttavia, la storia della cultura mondiale e non solo europea, mostra che sicuramente questa stessa idea, variata in modi diversi, veniva applicata già da secoli nei tracciati sacri Hindu noti come “yantra”, usati come ausilio alle pratiche di meditazione.
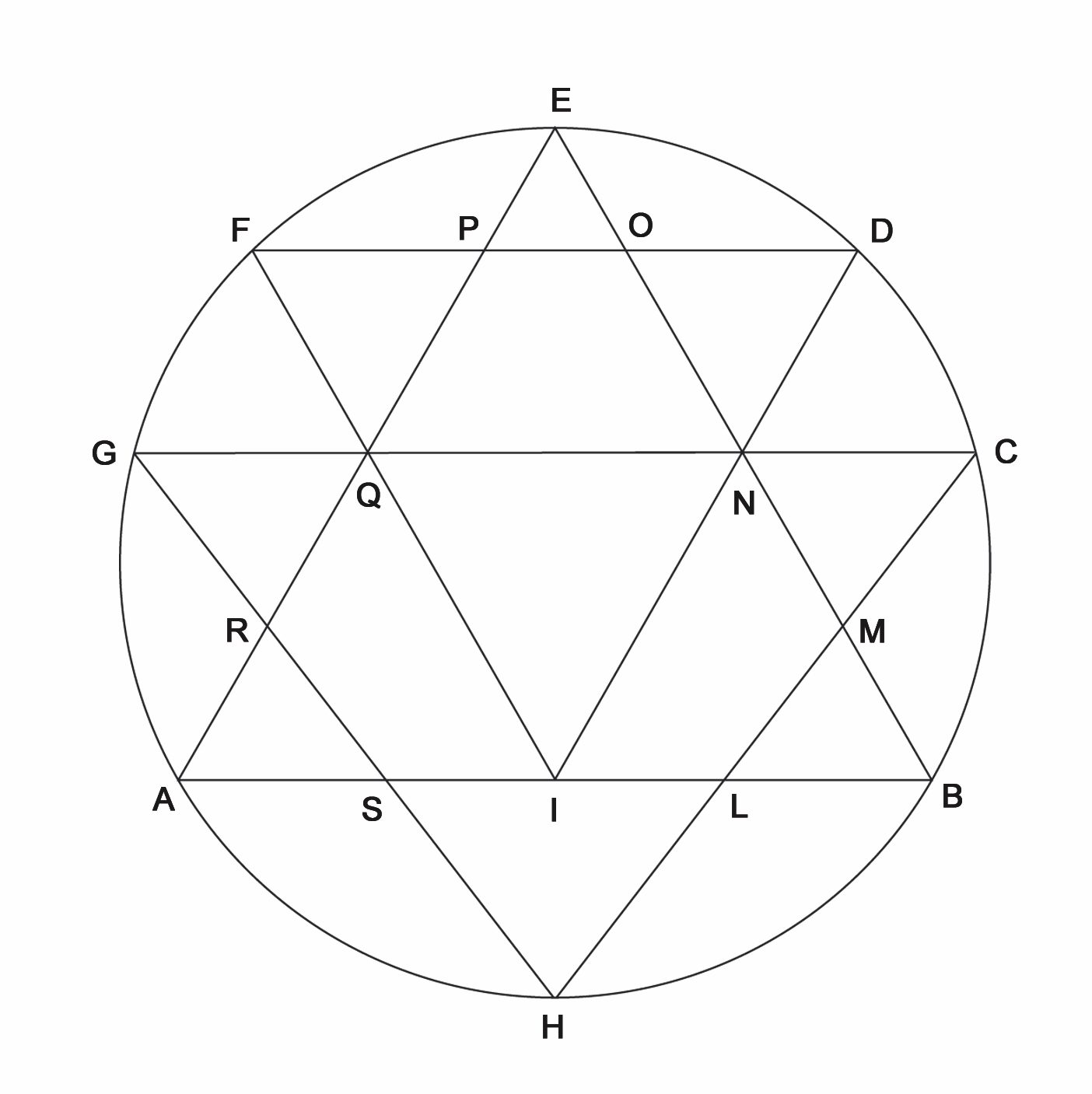
Ad esempio nel Nava Yoni Yantra dove il triangolo equilatero ABE inscritto nel cerchio viene suddiviso nel lato AE in sezione aurea nei segmenti successivi AQ, QP, PE (e simmetricamente sull’altro lato come BN, NO, OE), mentre la base AB viene intersecata dal triangolo isoscele CGH nei segmenti LS e AS che sono tra loro in sezione aurea (idem per SL e LB).
Erano queste idee geometriche una consapevole applicazione della sezione aurea, o sono dati “impliciti” nella costruzione dell’immagine?
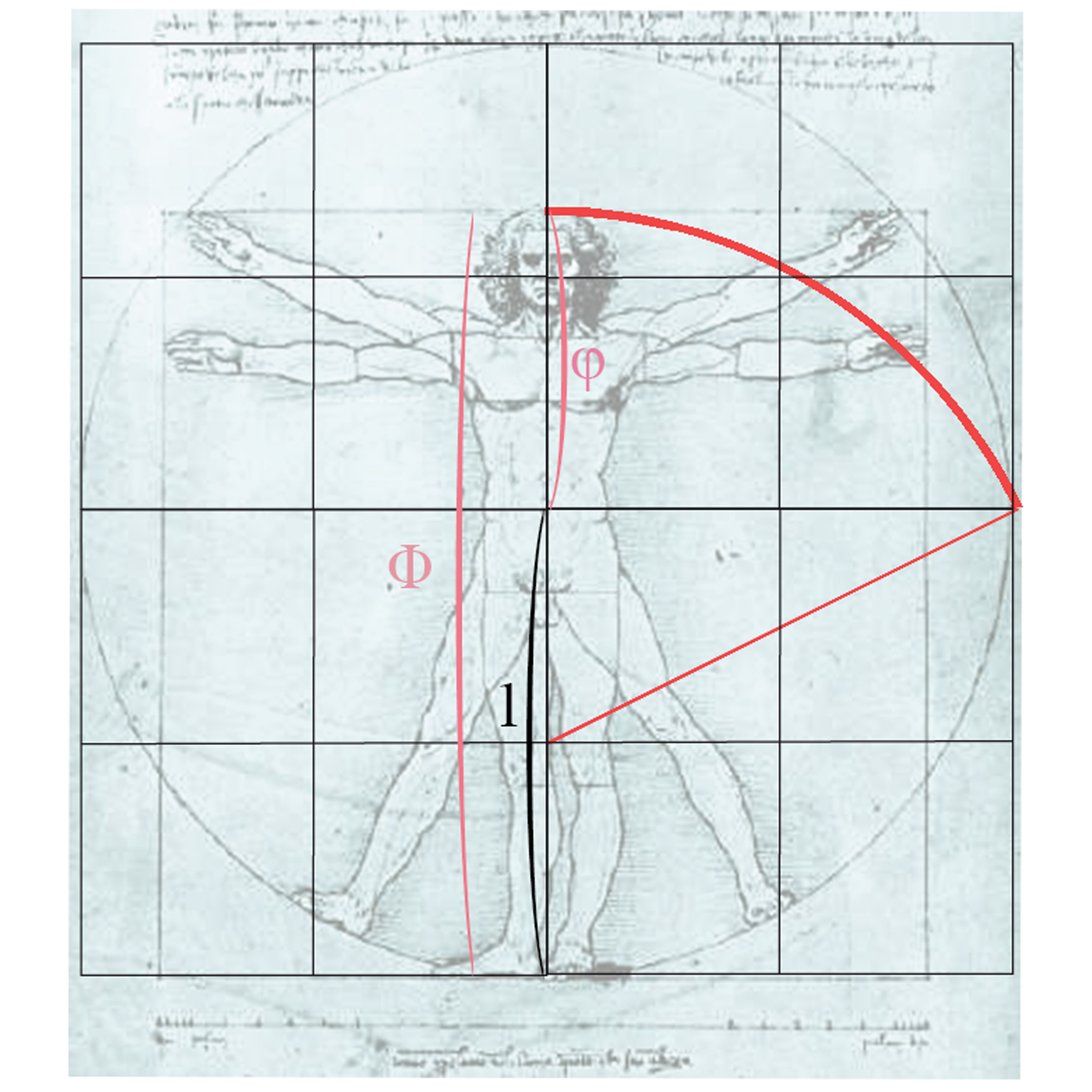
La stessa domanda vale per esempio per la famosa Grande Piramide di Cheope, che incorpora la sezione aurea nella sua stessa natura geometrica. Sono questi problemi storici ed ermeneutici che ci portano a interrogare su cosa veramente sappiamo di un dato argomento, e che cosa di conseguenza ne tramandiamo come conoscenze acquisite. Per tornare all’epoca di Pacioli, possiamo citare un altro mito culturale nel celeberrimo disegno dell’uomo vitruviano di Leonardo Da Vinci. Pacioli fece da tramite tra due sommi maestri del Rinascimento, tra Piero Della Francesca (da cui imparò la geometria, venendo poi accusato dal Vasari di averne plagiato il più famoso studio sulla sezione aurea, il De quinque corporibus regularibus) e venendo da questi anche ritratto nella famosa Pala di Brera, e Leonardo a cui insegnò la geometria, e che illustrò con i suoi famosi disegni di solidi in prospettiva il De Divina Proportione del 1509, il libro più famoso del frate matematico. Forse, a testimonianza di questo tramite, il famoso e controverso (nell’attribuzione) ritratto del Pacioli conservato oggi al Museo di Capodimonte a Napoli, potrebbe essere stato iniziato da Piero Della Francesca a Urbino e quindi terminato da Leonardo a Milano?

in secondo piano.
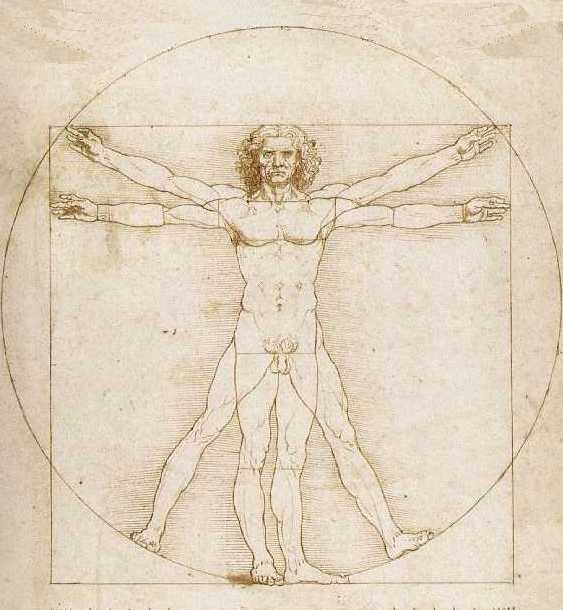
L’uomo vitruviano di Leonardo non è fatto con l’ausilio della sezione aurea, come anche esplicitato nel testo che lo accompagna e che, come dice il titolo, sviluppa le idee di Vitruvio. Leonardo apprenderà approfonditamente la sezione aurea da Pacioli quasi un decennio dopo, eppure la figura umana sembra suddivisa naturalmente in sezione aurea dall’ombelico. Sone regole scritte nella natura ed esplicitate genialmente nell’uomo ideale, come confermato già nel XIX secolo dalle ricerche pionieristiche sulla fisiologia e percezione umana da parte dello scienziato G. Fechner.
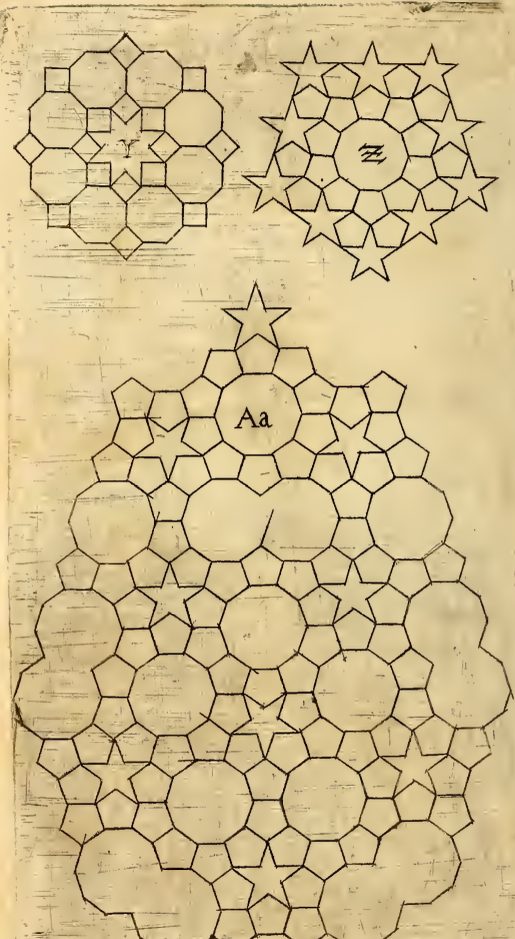
Qualcosa di simile, nella sovrapposizione del mito culturale alle cose che diamo per note, è legata alla vicenda del premio Nobel per la Chimica del 2011, dato al fisico israeliano D. Shechtman per la scoperta (nel 1984!) dei quasicristalli, ovvero di strutture di tassellazione del piano mediante parti di un pentagono. Il piano può essere riempito uniformemente solo con triangoli equilateri, quadrati ed esagoni, per cui l’evidenza di questa scoperta in natura di poter riempire il piano con due pezzi di pentagono ci mise un po’ di tempo ad essere pienamente accettata, anche se la sua teoria era già stata esplicitata dal fisico britannico R. Penrose negli anni 70 del XX secolo, e ancora prima nel 1619 da J. Kepler nel suo libro Harmonices Mundi, e prima ancora nelle decorazioni islamiche medievali, come scoperto dal fisico P.J. Lu.
Queste storie, sospese tra l’antico e il moderno, ci fanno capire quanto ci sia ancora da capire e da mettere in relazione, e soprattutto quanto ci sia da fare per riordinare le nostre conoscenze.

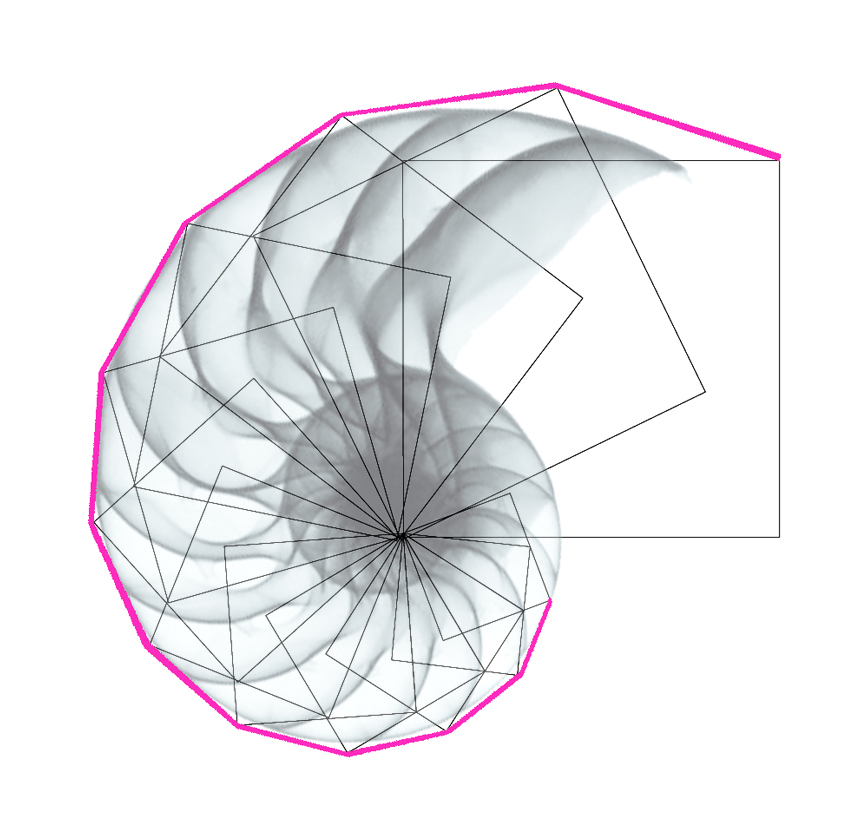
Un’altro esemplare mito culturale è quello legato alla crescita della spirale della conchiglia del bellissimo Nautilus pompilius. Questa, come le varie conchiglie a spirale, segue senz’altro uno sviluppo secondo una spirale logaritmica, che però non è direttamente sovrapponibile alla spirale aurea ricavabile dal rettangolo aureo (cioè con il lato minore sezione aurea del lato maggiore), come sovente divulgato. Tuttavia, alla conchiglia del Nautilus è sovrapponibile con una certa precisione una spirale di quadrati che segue il tracciato di crescita di un quarto della superficie dei quadrati successivi, esplicitata tramite uno gnomone aureo, mostrandoci un altro modo (ancora poco noto) con cui la sezione aurea crea tante strutture e forme della Natura…